This is a two part post, you can see part 2 here.

In my natural language processing class we've been playing around with similarity measures and I thought it would be useful to write them up here. Obviously this isn't an exhaustive list but I think it would be a good resource for anyone looking to learn a bit more about ways of measuring similarity between documents.

One of the first steps in many NLP operations is tokenization. Tokenization is the process by which we split a string into a list of "tokens" or words. While the below formula isn't exhaustive, it works well for simple things.

Here's the code in python:

from \_\_future\_\_ import division
import string
import math

tokenize = lambda doc: doc.lower().split(" ")

Now of course we'll need some documents.

document\_0 = "China has a strong economy that is growing at a rapid pace. However politically it differs greatly from the US Economy."
document\_1 = "At last, China seems serious about confronting an endemic problem: domestic violence and corruption."
document\_2 = "Japan's prime minister, Shinzo Abe, is working towards healing the economic turmoil in his own country for his view on the future of his people."
document\_3 = "Vladimir Putin is working hard to fix the economy in Russia as the Ruble has tumbled."
document\_4 = "What's the future of Abenomics? We asked Shinzo Abe for his views"
document\_5 = "Obama has eased sanctions on Cuba while accelerating those against the Russian Economy, even as the Ruble's value falls almost daily."
document\_6 = "Vladimir Putin was found to be riding a horse, again, without a shirt on while hunting deer. Vladimir Putin always seems so serious about things - even riding horses."

all\_documents = [document\_0, document\_1, document\_2, document\_3, document\_4, document\_5, document\_6]

tokenized\_documents = [tokenize(d) for d in all\_documents] # tokenized docs
all\_tokens\_set = set([item for sublist in tokenized\_documents for item in sublist])

These are just a random set of documents that I've written. Some are derived from some tweets that I read, others are just made up entirely. However we can see that there are some that are more similar to one another than others.

Jaccard Similarity

Jaccard Similarity is the simplest of the similarities and is nothing more than a combination of binary operations of set algebra. To calculate the Jaccard Distance or similarity is treat our document as a set of tokens. Mathematically the formula is as follows:

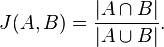
source: Wikipedia

It's simply the length of the intersection of the sets of tokens divided by the length of the union of the two sets.

In Python we can write the Jaccard Similarity as follows:

def jaccard\_similarity(query, document):
    intersection = set(query).intersection(set(document))
    union = set(query).union(set(document))
    return len(intersection)/len(union)

Here we are running it on a couple of the documents:

# comparing document\_2 and document\_4
jaccard\_similarity(tokenized\_documents[2],tokenized\_documents[4])
# 0.16666666666666666

We can see that these documents are a better match, but still far from perfect. There are a couple of things throwing us off. Document length has a big effect and common words carry the same weight as non common words. Let's take a look at the intersection to understand what I'm talking about.

set(tokenized\_documents[2]).intersection(set(tokenized\_documents[4]))
# {'abe', 'his', 'shinzo', 'the'}

As we can see, "his" and "the" have the same weight as "abe" and "shinzo". Let's take a more extreme example.

jaccard\_similarity(tokenized\_documents[1],tokenized\_documents[6])
# 0.08571428571428572
set(tokenized\_documents[1]).intersection(set(tokenized\_documents[6]))
# {'about', 'seems', 'serious'}

These documents have nothing in common. However they are rated as 8% relevant. This examples identifies the fundamental issues with Jaccard Similarity:

1. Length is irrelevant. (bias towards longer documents).
2. Words that appear in a lot of documents are weighted the same as those that appear in few. (bias towards longer documents as well as non-descriptive words)

We need a way to weigh certain words differently than others. Words that appear in all the documents are not going to be good at identifying documents because of the fact that, well...they appear in all the documents. Let's move onto another similarity measure that takes this into account TF-IDF and Cosine Similarity.

References:

• Jaccard Similarity on Wikipedia

TF-IDF

TF, or Term Frequency, measures one thing: the count of words in a document. It's the first step for TF-IDF or Term Frequency Inverse Document Frequency.

First comes the easy part.

def term\_frequency(term, tokenized\_document):
    return tokenized\_document.count(term)

Above we've created a simple way of counting the number of occurrences of a token in a document. There are plenty of ways to do this, through collections or for loops but they all end with the same result, how many times does a token appear in a document.

However this does not resolve the issue we've mentioned above - this is still biased towards longer documents. To remedy this we should weight terms according to document length or normalize them on another scale. This process is called normalization. While there are several ways to do this, I'll only show two, sub-linear term frequency and augmented frequency measurement. Here's the formula:

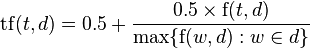
def sublinear\_term\_frequency(term, tokenized\_document):
    return 1 + math.log(tokenized\_document.count(term))

def augmented\_term\_frequency(term, tokenized\_document):
    max\_count = max([term\_frequency(t, tokenized\_document) for t in tokenized\_document])
    return (0.5 + ((0.5 \* term\_frequency(term, tokenized\_document))/max\_count))

These two different normalization techniques obviously approach our goal differently. I'll be focusing on the sub-linear term frequency as it will tie into exploring Tfidf with Scikit-Learn.

The next part of TF-IDF is the IDF or inverse document frequency. Basically we want to target the words that are unique to certain documents instead of those that appear in all the documents because by definition, those are not good identifiers for any given document. Here's our equation for IDF.

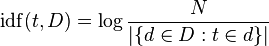
def inverse\_document\_frequencies(tokenized\_documents):
    idf\_values = {}
    all\_tokens\_set = set([item for sublist in tokenized\_documents for item in sublist])
    for tkn in all\_tokens\_set:
        contains\_token = map(lambda doc: tkn in doc, tokenized\_documents)
        idf\_values[tkn] = 1 + math.log(len(tokenized\_documents)/(sum(contains\_token)))
    return idf\_values

Now we've got a weight for every token in every document. This helps determine the important words from the unimportant ones.

idf\_values = inverse\_document\_frequencies(tokenized\_documents)
print idf\_values['abenomics']
# 2.94591014906
print idf\_values['the']
# 1.33647223662

Now we see the power of TF-IDF. We've taken the inverse of a token's document frequency. This means that words that appear a lot like "the" are weighted much less than words like "abenomics". However TF-IDF allows us to do so much more. We can create vector representations of sentences or more simply, we can transform documents into numbers and lists of documents into matrices.

While this seems relatively unimportant, it actually allows us to do a lot of exception things. We have a mathematical representation of a sentence and we can now use that representation in mathematical ways.

def tfidf(documents):
    tokenized\_documents = [tokenize(d) for d in documents]
    idf = inverse\_document\_frequencies(tokenized\_documents)
    tfidf\_documents = []
    for document in tokenized\_documents:
        doc\_tfidf = []
        for term in idf.keys():
            tf = sublinear\_term\_frequency(term, document)
            doc\_tfidf.append(tf \* idf[term])
        tfidf\_documents.append(doc\_tfidf)
    return tfidf\_documents

Now that we've got a way of performing tfidf, let's run it!

tfidf\_representation = tfidf(all\_documents)
print tfidf\_representation[0], document\_0
# doc vector and document

These two representations are functionally equivalent at this point. Now up until this point we've done all this by hand, while it's been a good exercise there are packages that implement this much more quickly - like Scikit-Learn.

Let's take a look at how we might code this in Scikit-Learn.

from sklearn.feature\_extraction.text import TfidfVectorizer

sklearn\_tfidf = TfidfVectorizer(norm='l2',min\_df=0, use\_idf=True, smooth\_idf=False, sublinear\_tf=True, tokenizer=tokenize)

sklearn\_representation = sklearn\_tfidf.fit\_transform(all\_documents)
print tfidf\_representation[0]
print sklearn\_representation.toarray()[0].tolist()
print document\_0

While you will notice that the values in each matrix are not the same because Scikit-learn presents the IDF ordering in a different way (in that fitted model). However we can see in the next part of this tutorial that the exact numbers are irrelevant, it is the vectors that are important. The next post focuses on cosine similarity or the Euclidean dot product formula in python.

Here's all of our code so far:

from **future** import division
import string
import math

tokenize = lambda doc: doc.lower().split(" ")

document0 = "China has a strong economy that is growing at a rapid pace. However politically it differs greatly from the US Economy." document1 = "At last, China seems serious about confronting an endemic problem: domestic violence and corruption." document2 = "Japan's prime minister, Shinzo Abe, is working towards healing the economic turmoil in his own country for his view on the future of his people." document3 = "Vladimir Putin is working hard to fix the economy in Russia as the Ruble has tumbled." document4 = "What's the future of Abenomics? We asked Shinzo Abe for his views" document5 = "Obama has eased sanctions on Cuba while accelerating those against the Russian Economy, even as the Ruble's value falls almost daily." document_6 = "Vladimir Putin is riding a horse while hunting deer. Vladimir Putin always seems so serious about things - even riding horses. Is he crazy?"

all*documents = document0, document1, document2, document3, document4, document5, document*6

def jaccard_similarity(query, document): intersection = set(query).intersection(set(document)) union = set(query).union(set(document)) return len(intersection)/len(union)

def termfrequency(term, tokenizeddocument): return tokenized_document.count(term)

def sublineartermfrequency(term, tokenizeddocument): count = tokenizeddocument.count(term) if count == 0: return 0 return 1 + math.log(count)

def augmentedtermfrequency(term, tokenizeddocument): maxcount = max(termfrequency(t, tokenizeddocument) for t in tokenized*document) return (0.5 + ((0.5 * termfrequency(term, tokenizeddocument))/max*count))

def inversedocumentfrequencies(tokenizeddocuments): idfvalues = {} alltokensset = set(item for sublist in tokenized*documents for item in sublist) for tkn in alltokensset: containstoken = map(lambda doc: tkn in doc, tokenizeddocuments) idfvaluestkn = 1 + math.log(len(tokenizeddocuments)/(sum(contains*token))) return idf_values

def tfidf(documents): tokenizeddocuments = tokenize(d) for d in documents idf = inversedocumentfrequencies(tokenizeddocuments) tfidfdocuments = for document in tokenizeddocuments: doctfidf = for term in idf.keys(): tf = sublineartermfrequency(term, document) doctfidf.append(tf * idfterm) tfidfdocuments.append(doctfidf) return tfidf_documents

in Scikit-Learn

from sklearn.feature_extraction.text import TfidfVectorizer

sklearntfidf = TfidfVectorizer(norm='l2',mindf=0, useidf=True, smoothidf=False, sublineartf=True, tokenizer=tokenize) sklearnrepresentation = sklearntfidf.fittransform(all_documents)

Further References:

• TF-IDF
• Scikit-Learn TF-IDF